| початок розділу
Виробничі, аматорські радіоаматорські Авіамодельний, ракетомодельного Корисні, цікаві |
хитрощі майстру
електроніка фізика технології винаходи |
таємниці космосу
таємниці Землі таємниці Океану хитрощі Карта розділу |
|
| Використання матеріалів сайту дозволяється за умови посилання (для сайтів - гіперпосилання) | |||
Навігація: => |
На головну / Винаходи / Нові типи двигунів / |
|
ЧУДО-КОЛЕСО АБО "PERPETUUM MOBILE"?
- ОСНОВИ ГЕОМЕТРІЇ -
Дивись також: |
Коло в геометрії є простою фігурою з відомими формулами для знаходження площі і довжини окружності. Формулювання звучить як фігура, у якої відстані від центру до будь-якої точки на колі рівні. Це відстань позначається радіусом "R" і є вихідним для побудови кола. Після знаходження числа "Пі" ця фігура стала більш зрозумілою і ясною. Правильність і математичне досконалість кола привертає, а й обмежує його у використанні.
Запропонуємо іншу фігуру, назвемо кругом і постараємося довести, що це коло. Для встановлення родинних відносин спочатку змінимо саме сприйняття кола прибравши його складову-радіус. І головне формулювання цієї фігури з радіусної на діаметральну. Кругом називається фігура, у якої все прямі перетинають її в центрі рівні. Поміняємо і формулу знаходження площі з радіусної на діаметральну. Площа круга дорівнює (периметр помножити на діаметр) і розділити на чотири. Слово периметр не випадково, оскільки ця формула дає площа і інший
фігури-квадрата. Периметр і довжина кола і сума всіх сторін квадрата. За діаметр приймемо і довжину квадрата. Площа круга і квадрата можна зв'язати і відсотками. Площа круга становить 78,5% від площі квадрата в який вписується даний коло. Але основне для подальших побудов, це формулювання обходиться без радіуса.
Для створення нового кола знадобиться нескладний геометричний інструмент зображений на малюнку.

геометричний інструмент
Це прозорий брусок, виконаний з органічного скла, у вигляді високої лінійки. Посередині наскрізний, поздовжній лаз з двома легкими олівцями, які легко зупиняти на потрібних точках. Між ними, і вільно ковзає, штир з пристосуванням дозволяє притискати інструмент до креслярського аркуша. Крім використання інструменту як лінійки, його можливо використовувати і як циркуль. Скориставшись штирем і одним олівцем (або двома але рівновіддаленими від нього) отримаємо циркуль. Але основне його застосування використання як «дзеркало», полягає в наступному.
Візьмемо одну з простих фігур - квадрат і перетином діагоналей знайдемо центр встановимо на ньому штир і закріпимо олівці в діагональних кутах. Потім, притискаючи штир, проведемо одним олівцем по всьому периметру квадрата і отримаємо його відображення іншим олівцем.
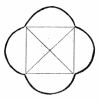
Дивись фотографію прикладу побудови
Таким же чином використовуючи цей інструмент, тобто взявши максимальну пряму, що перетинає фігуру в центрі отримаємо цікаві результати.
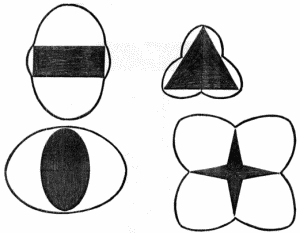
Схожими фігурами, на відміну від їх математичних "родичів", користується природа, створюючи різні види флори і фауни.
Виходячи від зворотного, взявши деякі види організмів або рослин, можна поповнити геометричний арсенал фігур. Але причому тут механіка і коло? Коло це єдина фігура не дає відображення, або точніше сказати вони повністю повідомлені - коло зі своїм відображенням. яка надається фігура теж поєднана зі своїм відображенням, так як є теж кругом. Для виключення плутанини в подальшому, будемо називати звичайний коло - радіусом (або мертвим) колом. Математично, по єдиному відрізняю від такого кола, подану фігуру правильніше називати без радіусним колом.
Для спрощення демонстрації його створення, візьмемо за основу радісний коло.
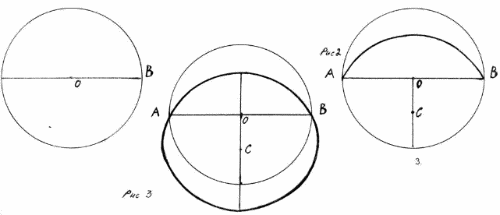
Прокреслити горизонтальну пряму "АВ" перетинає центр "О" рис.1. З цієї точки опустимо перпендикуляр і виберемо будь-яку точку "С" на ньому. Встановивши в цій (назвемо її точкою відображення) точці циркуль, з'єднаємо точки А і В рис.2. Тепер скориставшись нашим інструментом - дзеркалом, отримаємо відображення кривої "АВ" через центр "О" який замкнув її (рис. 3). Таким чином ми отримали шукану фігуру- коло з діаметром рівним колі з якого почали роботу.
Подібну фігуру можна отримати відображенням тривимірного радіусного кола на
двомірної площини, прийом відомий всім художникам.
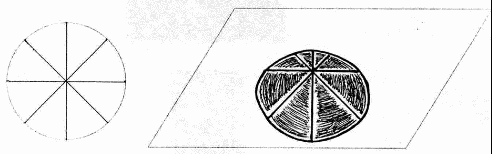
Крапку "С" можна вибрати і на перетині перпендикуляра з колом, і можна за колом. Максимальне видалення від центру точки "С" це відстань діаметра.
З центру радіусного кола опустимо перпендикуляр за окружність, візьмемо циркулем відстань "АВ" та з тачки А чи В і відзначимо на перпендикуляре точку "С". Отримаємо максимально можливий радісний коло (рис.1). При збільшенні відстані коло переходить в іншу фігуру (рис.2).
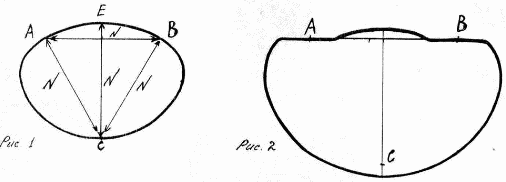
У максимального кола точка відображення "С" виявляється на окружності без радісних кола оскільки ми взяли діаметр кола за Циркульні відстань для побудови без радісних кола (рис.1). Поєднуючи точки А і В циркулем з точки "С" з'являється точка "Е" з відстанню з точки "С" рівну відстані АВ і ВС. Але радіус не може бути рівним діаметру. Крім того, пряма АВ (рис.1) ділить і без радісний коло посередині, але не по площі а за кількістю точок складових коло.
Парадоксально, так як друга половина окружності ВА має значно більшу довжину ніж АВ. Залишаючись замкнутою фігурою, доводиться стверджувати, що точки на половині ВА більше по довжині, ніж протилежні їм на половині АВ.
Стверджувати про рівність площі квадрата, зі стороною рівною діаметру кола, з площею без радісних кола, і як і про рівність довжини окружності з периметром немає даних. Проста комп'ютерна програма для геометричних побудов знаходження площ довжин кіл і периметрів не знайшла.
Будемо вважати доведеним існування без радісних кола. Зупинимося на цьому в математичних блукання і суперечках, і практично доведемо що це все таки коло, вірніше колесо здатне обертатися.
Версія для друку
Автор: Elman Jamilov
PS Матеріал захищений.
Дата публікації 02.25.2004гг




Коментарі
Коментуючи, пам'ятайте про те, що зміст і тон Вашого повідомлення можуть зачіпати почуття реальних людей, проявляйте повагу та толерантність до своїх співрозмовників навіть у тому випадку, якщо Ви не поділяєте їхню думку, Ваша поведінка за умов свободи висловлювань та анонімності, наданих інтернетом, змінює не тільки віртуальний, але й реальний світ. Всі коменти приховані з індексу, спам контролюється.